Beranda  ›  180 Degree Consulting There Was an Error While Uploading the File. Error Code: 7

180 Degree Consulting There Was an Error While Uploading the File. Error Code: 7

Ditulis Senin, 11 April 2022 Tulis Komentar Edit

Program to calculate the value of sin(x) and cos(x) using Expansion

Given a value of angle, you need to calculate Sin and Cos values respective to information technology.

For sin function

Examples:

Input : 90 Output : 1

{\displaystyle Sin(x)=\sum_{k=0}^{\infty } \frac {(-1)^k}{(2k+1)!}x^{2k+1}=x-\frac {x^3}{3!} + \frac {x^5}{5!} - .........}

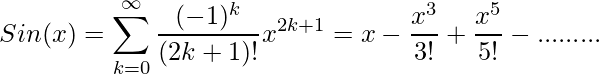
C++

#include <iostream>

#include <math.h>

using namespace std;

void cal_sin( float n)

{

float accuracy = 0.0001, denominator, sinx, sinval;

n = n * (3.142 / 180.0);

float x1 = n;

sinx = due north;

sinval = sin (north);

int i = 1;

do

{

denominator = 2 * i * (2 * i + 1);

x1 = -x1 * due north * n / denominator;

sinx = sinx + x1;

i = i + 1;

} while (accuracy <= fabs (sinval - sinx));

cout << sinx;

}

int master()

{

float north = xc;

cal_sin(n);

return 0;

}

Java

import static java.lang.Math.sin;

form GFG {

static void cal_sin( bladder n)

{

float accuracy = ( float ) 0.0001 , denominator, sinx, sinval;

north = n * ( bladder )( iii.142 / 180.0 );

bladder x1 = due north;

sinx = n;

sinval = ( bladder )sin(due north);

int i = 1 ;

do

{

denominator = two * i * ( two * i + 1 );

x1 = -x1 * n * n / denominator;

sinx = sinx + x1;

i = i + one ;

} while (accuracy <= sinval - sinx);

System.out.println(sinx);

}

public static void master(Cord[] args) {

float n = 90 ;

cal_sin(n);

}

}

Python3

import math;

def cal_sin(due north):

accuracy = 0.0001 ;

north = north * ( 3.142 / 180.0 );

x1 = n;

sinx = n;

sinval = math.sin(n);

i = 1 ;

while ( True ):

denominator = 2 * i * ( 2 * i + 1 );

x1 = - x1 * n * n / denominator;

sinx = sinx + x1;

i = i + 1 ;

if (accuracy < = abs (sinval - sinx)):

intermission ;

print ( circular (sinx));

north = ninety ;

cal_sin(due north);

C#

using Organisation;

class GFG

{

static void cal_sin( float n)

{

bladder accuracy = ( float ) 0.0001,

denominator, sinx, sinval;

n = north * ( float )(three.142 / 180.0);

float x1 = n;

sinx = due north;

sinval = ( float )Math.Sin(northward);

int i = one;

practise

{

denominator = 2 * i * (2 * i + 1);

x1 = -x1 * n * north / denominator;

sinx = sinx + x1;

i = i + 1;

} while (accuracy <= sinval - sinx);

Panel.WriteLine(sinx);

}

static public void Primary ()

{

float n = 90;

cal_sin(n);

}

}

PHP

<?php

function cal_sin( $n )

{

$accuracy = 0.0001;

$northward = $due north * (3.142 / 180.0);

$x1 = $n ;

$sinx = $north ;

$sinval = sin( $n );

$i = 1;

do

{

$denominator = two * $i * (2 * $i + one);

$x1 = - $x1 * $n * $n / $denominator ;

$sinx = $sinx + $x1 ;

$i = $i + one;

} while ( $accurateness <= abs ( $sinval - $sinx ));

echo round ( $sinx );

}

$north = 90;

cal_sin( $n );

?>

Javascript

<script>

role cal_sin(n) {

var accuracy =  0.0001, denominator, sinx, sinval;

north = n *  (iii.142 / 180.0);

var x1 = due north;

sinx = n;

sinval =  Math.sin(northward);

var i = one;

do {

denominator = 2 * i * (2 * i + 1);

x1 = -x1 * n * n / denominator;

sinx = (sinx + x1);

i = i + i;

} while (accurateness <= sinval - sinx);

document.write(sinx.toFixed(0));

}

var n = 90;

cal_sin(due north);

</script>

Output:

1

For cos function

Examples:

Input : thirty Output : 0.86602

{\displaystyle Cos(x)=\sum_{k=0}^{\infty } \frac {(-1)^k}{(2k)!}x^{2k}=1-\frac {x^2}{2!} + \frac {x^4}{4!} -.....}

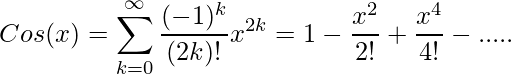
C++

#include <iostream>

#include <math.h>

using namespace std;

void cal_cos( float northward)

{

float accurateness = 0.0001, x1, denominator, cosx, cosval;

n = n * (three.142 / 180.0);

x1 = 1;

cosx = x1;

cosval = cos (north);

int i = 1;

do

{

denominator = 2 * i * (2 * i - one);

x1 = -x1 * n * n / denominator;

cosx = cosx + x1;

i = i + 1;

} while (accuracy <= fabs (cosval - cosx));

cout << cosx;

}

int main()

{

bladder n = 30;

cal_cos(n);

}

Coffee

import static java.lang.Math.cos;

class GFG {

static void cal_cos( float north) {

float accuracy = ( float ) 0.0001 , x1, denominator, cosx, cosval;

north = n * ( float ) ( iii.142 / 180.0 );

x1 = 1 ;

cosx = x1;

cosval = ( float ) cos(due north);

int i = 1 ;

practise {

denominator = 2 * i * ( ii * i - 1 );

x1 = -x1 * n * n / denominator;

cosx = cosx + x1;

i = i + i ;

}

while (accurateness <= cosval - cosx);

Organisation.out.println(cosx);

}

public static void main(String[] args) {

float n = 30 ;

cal_cos(northward);

}

}

Python3

from math import fabs, cos

def cal_cos(n):

accuracy = 0.0001

due north = n * ( 3.142 / 180.0 )

x1 = 1

cosx = x1

cosval = cos(n)

i = 1

denominator = two * i * ( two * i - ane )

x1 = - x1 * n * n / denominator

cosx = cosx + x1

i = i + 1

while (accuracy < = fabs(cosval - cosx)):

denominator = ii * i * ( 2 * i - 1 )

x1 = - x1 * n * n / denominator

cosx = cosx + x1

i = i + one

print ( '{0:.6}' . format (cosx))

if __name__ = = '__main__' :

n = 30

cal_cos(due north)

C#

using Organisation;

class GFG {

static void cal_cos( float northward) {

bladder accurateness = ( float ) 0.0001, x1, denominator, cosx, cosval;

n = n * ( bladder ) (three.142 / 180.0);

x1 = ane;

cosx = x1;

cosval = ( bladder ) Math.Cos(due north);

int i = one;

practise {

denominator = two * i * (two * i - ane);

x1 = -x1 * n * northward / denominator;

cosx = cosx + x1;

i = i + 1;

}

while (accurateness <= cosval - cosx);

Console.WriteLine(cosx);

}

static void Main() {

float north = 30;

cal_cos(due north);

}

}

PHP

<?php

function cal_cos( $n )

{

$accuracy = 0.0001;

$n = $n * (iii.142 / 180.0);

$x1 = ane;

$cosx = $x1 ;

$cosval = cos ( $due north );

$i = 1;

do

{

$denominator = 2 * $i * (two * $i - 1);

$x1 = - $x1 * $due north * $northward / $denominator ;

$cosx = $cosx + $x1 ;

$i = $i + i;

} while ( $accuracy <= abs ( $cosval - $cosx ));

echo circular ( $cosx , 6);

}

$due north = 30;

cal_cos( $north );

?>

Javascript

<script>

part cal_cos(n)

{

permit accurateness = 0.0001, x1, denominator, cosx, cosval;

due north = n * (3.142 / 180.0);

x1 = ane;

cosx = x1;

cosval = Math.cos(n);

allow i = one;

do

{

denominator = 2 * i * (2 * i - ane);

x1 = -x1 * n * n / denominator;

cosx = cosx + x1;

i = i + 1;

} while (accurateness <= Math.abs(cosval - cosx));

document.write(cosx.toFixed(v));

}

let north = 30;

cal_cos(n);

</script>

Output:

0.86602

This article is contributed by Sakshi Tiwari. If you like GeeksforGeeks(Nosotros know yous do!) and would similar to contribute, yous tin can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. Run across your article appearing on the GeeksforGeeks main folio and assistance other Geeks.
Please write comments if yous find anything incorrect, or y'all want to share more information near the topic discussed in a higher place.


hakesrowleted56.blogspot.com

Source: https://www.geeksforgeeks.org/program-to-calculate-the-value-of-sinx-and-cosx-using-expansion/

Belum ada Komentar untuk "180 Degree Consulting There Was an Error While Uploading the File. Error Code: 7"

Posting Komentar

Langganan: Posting Komentar (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel